Audio Devices: Amplifier, Microphone, Antenna, Speaker Symbol

Hi, in this article we are going to see different types of audio devices symbols, and diagrams. Audio devices are coming under electronics engineering. So if you are an electronics engineering student, teacher, engineer, or any professional, then you must know these symbols and diagrams. Knowing these symbols, you can easily understand any circuit diagrams or wiring diagrams.

Generic Symbol of Amplifier

Here, you can see the generic symbol that can be used in any circuit diagrams or wiring diagrams to indicate an amplifier.

Op-Amp or Operational Amplifier Symbol

Operational amplifiers are those that have so many functions that means they can filter the electronic signals, amplify the electronic signal, generate the pulse signal.

Differential Amplifier Symbol

Differential amplifiers are those that take two different electronic signals as their input. First, they produce a differentiated signal and amplify it. Here, you can see the symbol of a differential amplifier.

Read Also: Most Important Electronic Symbols and Diagrams

High-Frequency Amplifier Symbol

High-Frequency Amplifiers are those which work with high-frequency electronic signals.

Low-Frequency Amplifier Symbol

Low-Frequency Amplifiers are those which work with low-frequency electronic signals.

Feedback Amplifier Symbol

Feedback amplifiers are those which have a feedback path from the output to input. Generally, they work in a closed-loop system.

Read Also: All Types of Electrical and Electronic Switch Symbol

Speaker Symbol

Speaker is a device that converts electrical energy into sound energy. Speaker works with electromagnet. When an audio signal is supplied to a speaker, it makes a sound. Here, you can see the symbol of speaker.

Audio Symbol

In some projects, presentations, the symbol of audio is used. It is just a round circle on a speaker symbol.

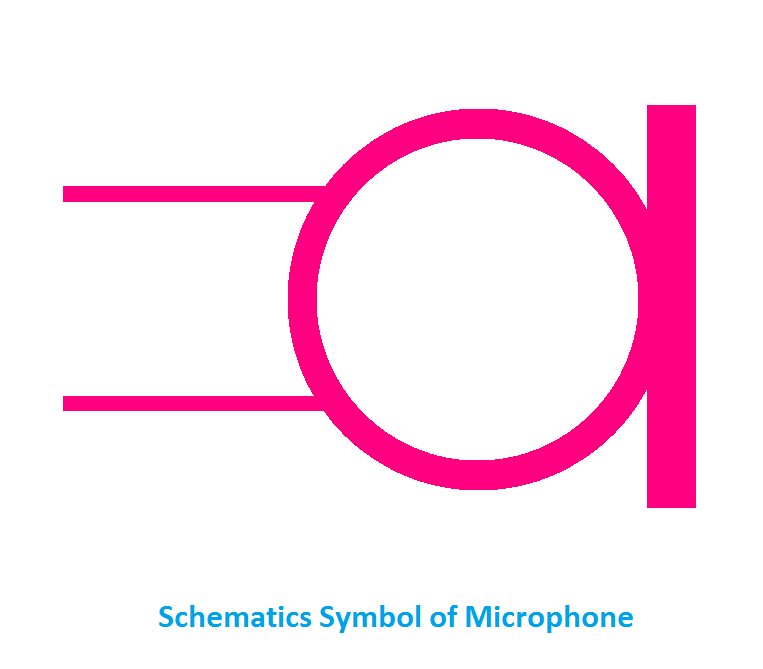
Schematics Symbol of Microphone

A microphone is a device that converts our voice or sound energy into electrical energy. it just opposite the speaker. A microphone also is called a transducer. Here, you can see the microphone symbol used in all the electronics circuit diagrams, wiring diagrams.

Read Also: Difference between Analogue, Digital, and Power Electronics

Microphone Symbol Icon

Here, you can see the icon symbol of microphone that is used in presentations, posters, etc.

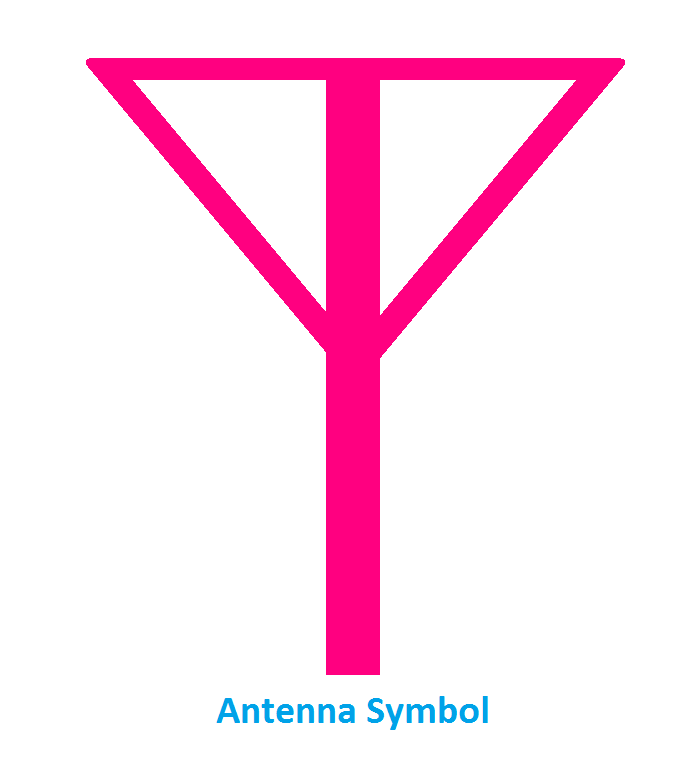
Antenna Symbol

An antenna is a device that helps to send or receive radio frequency signals. The antenna is used when audio signals are transmitted in the form of a radiofrequency signal wirelessly. Here, you can see the symbol of Antenna.

Read Also: 

• RJ45 Pinout Diagram, Colour Code and Terminal Identification
• What is Common Emitter Configuration in Transistor Amplifier?
• [Exact] Difference between Coupling Capacitor and Bypass Capacitor

Thank you for visiting the website. keep visiting for more updates.