Impedance Formula and Theory Explanation

Impedance Formula and Theory

When we talk about AC circuits the term Impedance comes. Impedance is a very known term to us. Today we are going to know the Impedance Formula and Theory with the explanation. In AC circuits impedance is always present.

Understanding What is Impedance practically:

To better understand Impedance we should know about Inductive Reactance and Capacitive Reactance.
We know that the resistor has the property of opposition to the flow of current. But how do inductors and capacitors oppose the flow of current? let's know.

Inductive Reactance:

The property of an inductor by virtue of which it offered opposition only to the flow of alternating current is called Inductive Reactance.

Remember that inductive reactance only exists in the AC circuit, not in DC.
Actually, each Inductor has a property of opposition to the flow of current (AC & DC both) according to their material property, this is called resistance. But the inductance reactance property only exists when the AC applies to it.
So we can say the capacity of an Inductor to oppose the flow of current in an AC circuit is greater than the DC circuit.

Capacitive Reactance:

The concept of capacitive reactance is the same as inductive reactance.
The property of a capacitor by virtue of which it offered opposition only to the flow of alternating current is called Capacitive Reactance.
Capacitive reactance also does not exist in DC circuits.

Reactance:

If an AC series circuit containing only Inductor and a capacitor does not contain Resistor, then the opposition offered by the combination of inductor and capacitor to the flow of alternating current is called Reactance(X).

Impedance:

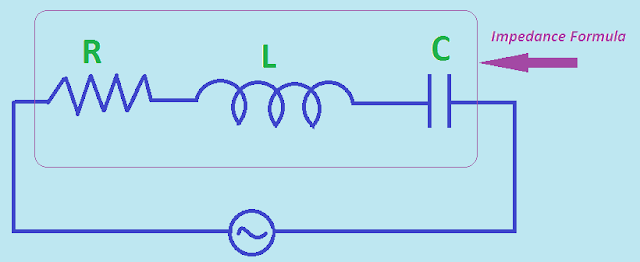
A series AC circuit which contains Resistor, Inductor, and Capacitor. Now the opposition offered by the combination of Resistor, Inductor, and Capacitor to the flow of AC current which flows through it is called Impedance.

Now let's go to the Impedance Formula.

Impedance Formula:

The basic impedance formula is, 

As the resistance=R, and the reactance=X
so the angle between the voltage and current of the circuit will be,

For a purely resistive circuit, the impedance will be, Z=R
For a purely Inductive circuit, the impedance will be, Z= X_L
For a purely Capacitive circuit, the impedance will be, Z= X_C

For the R-L circuit,

The  reactance=inductive reactance
so the impedance formula will be,

For the R-C circuit,

The reactance=capacitive reactance
so the impedance formula will be,

For the R-L-C circuit,
if X_L>X_C

impedance, 

If X_L<X_C
impedance,

If X_L=X_C
The impedance, Z=R

The impedance formula in complex form,

The formula for Total Impedance in Series: Ztotal = Z1 + Z2 + Z3 + ...

When multiple components are connected in series, the total impedance (Ztotal) is the sum of the individual impedances (Z1, Z2, Z3, ...) of each component.

The formula for total Impedance in Parallel: 1/Ztotal = 1/Z1 + 1/Z2 + 1/Z3 + ...

When multiple components are connected in parallel, the inverse of the total impedance (1/Ztotal) is equal to the sum of the inverses of the individual impedances (1/Z1, 1/Z2, 1/Z3, ...) of each component.

The formula for Impedance Matching: Zsource = Zload

Impedance matching is often desired in electrical circuits to ensure maximum power transfer. For optimal power transfer, the impedance of the source (Zsource) should be equal to the impedance of the load (Zload). So, when the impedance impedance of the source circuit is equal to the impedance of the load, the maximum power will be transferred from the source to load.

Read Also:

• Power Factor Formula Explanation
• All Inductance Formula Analysis
• Electrical Power Theory and Formula Explanation
• Capacitance Formula | All Formulas and Equations Explain
• Resistance Formula | All Formulas and Equations Explain

Thank you for visiting the website. keep visiting for more updates.