What is Amplitude of a Wave? Definition, Formula, Example
In simple words, the amplitude of a wave is the measurement of maximum displacement or changes of the variable from a particular reference point. If you want to easily understand the concept of the amplitude of a wave then you must have a clear idea of the wave. Actually, the waveform is a graphical representation of changing variables with respect to time. For example, a sinusoidal wave represents how the AC voltage decreases and increases over time. So here the definition of amplitude will be the maximum changes of voltage with respect to a reference point it may be zero potential. In our 230V sinusoidal waveform, the voltage decreases or increases from zero potential sometimes it goes to +230V and sometimes it goes to -230V. This change from 0V to 230V is expressed as the amplitude of that sinusoidal waveform.
Remember that, the amplitude represents the maximum value of an electrical signal. It indicates the strength or magnitude of the signal, which is essential for the proper functioning of electronic devices. A strong signal ensures that the information carried by the wave can be accurately transmitted and received. In alternating current (AC) circuits, the amplitude of the voltage or current wave determines the peak values, which are crucial for understanding the power delivery capacity and voltage compatibility of electrical components and devices.
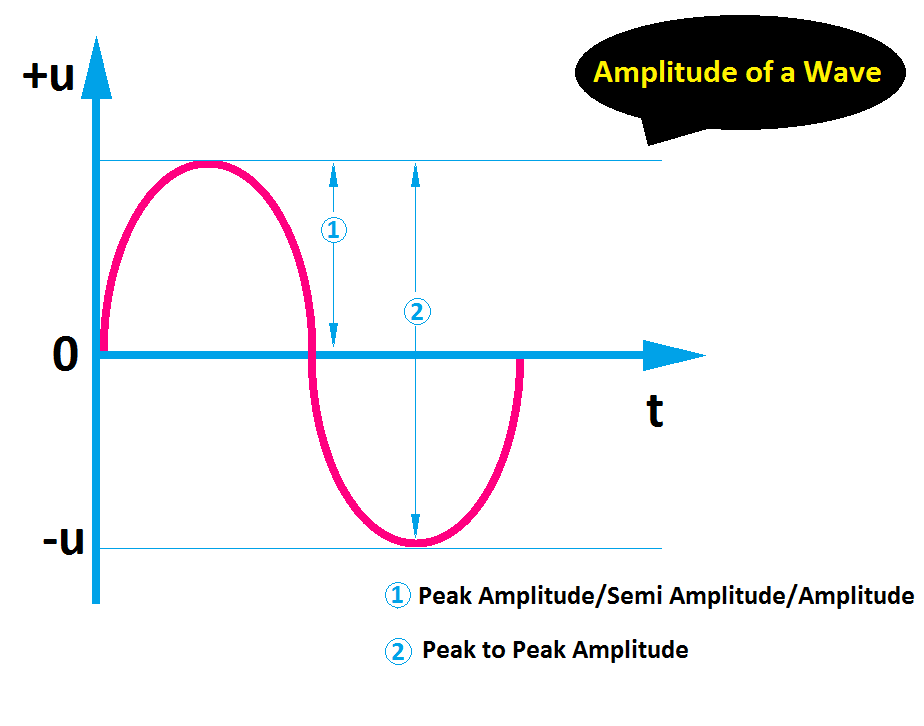
Here you can see the below diagram to understand the concept of amplitude.
As we know the amplitude is measured from a reference point, so according to it there are different types of amplitude.
For example, The peak amplitude refers to the maximum changes of the variable from the zero or center point. The peak amplitude is measured if the wave is not sinusoidal and the measured swings above and below a reference point. In the audio systems and radio communication systems, this type of amplitude is measured. The peak amplitude is generally termed amplitude or semi-amplitude (because it is half of the peak-to-peak amplitude).
Peak-to-peak amplitude can be measured between the maximum positive value and the maximum negative value. For a sinusoidal wave peak to peak, the amplitude can be measured easily because here the time period is equal.
Another format for measuring amplitude is Root Means Square Amplitude. The root means square amplitude is measured for complicated signals that have discrete waveforms such as noise signals.
Understand Amplitude with Examples
For example, in a sound wave, the amplitude is the maximum loudness or displacement of vibrating particles through the medium with respect to a mean point. So the loudness is directly proportional to the amplitude of the sound wave. As the sound wave is not sinusoidal so here mostly the peak amplitude or semi amplitude is measured.
The formula of Amplitude of a Wave
The simple equation or formula for amplitude is,
x = A sin (ωt + ϕ) or x = A cos (ωt + ϕ)
Here,
x = displacement of wave (meter)
A = amplitude
ω = angular frequency (rad/s)
t = time period
Ï• = phase angle
So, when finding amplitude, the above terms are very important. The time period is the time taken by the variable to complete a cycle. The number of cycles per second is known as frequency. Frequency is measured in Hertz.
Also, you should have knowledge about crest and trough. The crest is the maximum positive value whereas the trough is the maximum negative value.
Finding or having knowledge of amplitude is very important. Especially, some protective devices are designed to sense this amplitude. When the amplitude is higher than a certain value, it will trip or disconnect the system. For example, we have a device that will disconnect the circuit or trip when it senses a voltage of more than 300V. So when the voltage is normal means around 230V, it does not do anything but when the voltage exceeds 300V it trips the circuit. What is this 230V, 300V? These are the amplitude although we measure with an average value.
Read Also:
What is Amplitude of a Wave? Definition, Formula, Example
Reviewed by Author
on
April 20, 2022
Rating:
Reviewed by Author
on
April 20, 2022
Rating: